数値のデジタル化：１０進数から２進数に変える方法

コンピュータは私たちが普段使っている１０進数ではなく、２進数で情報を扱っています。
情報Iでは２進数に関する問題が多く出てくるので10進数↔︎2進数の変換ができるようにしておきましょう！

共通テストでもこの計算ができないと解けない問題もあります！
共テ対策の人も、定期テスト対策の人もしっかり覚えておきましょう！

10進数を2進数にする（整数）

元の数を２で割ったあまりを出していく

試しに19を2進数に直してみましょう。

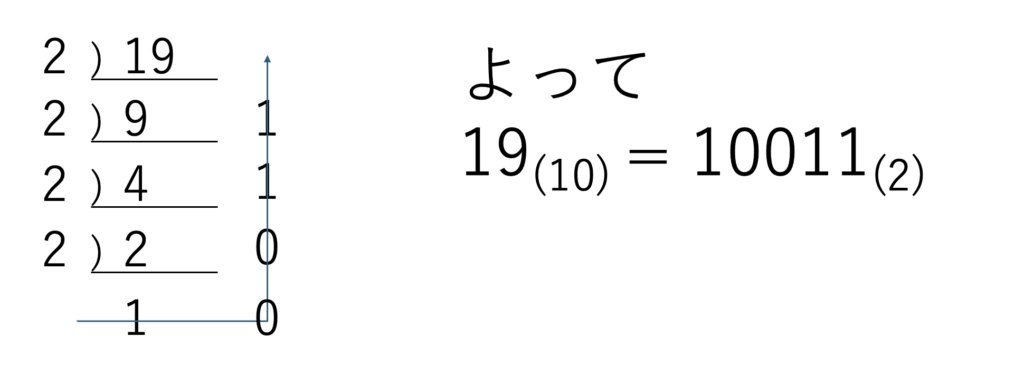
上の筆算をみてください。
19を2で割って9余り1
9を2で割って4余り1
4を2で割って2余り0
2を2で割って1余り0

と19の下に筆算のように書いていきます。

するとなんということでしょう！
欲しかった２進数が最後の商と、あまりのところに出てきています！

これを矢印の方向に下から書けば見事2進数への変換は終わりです。

10進数を2進数にする（少数）

さて、ここからは少数部分の話をします。
整数部分は2で割り算をして、筆算を下から読めば答えが出ましたが、少数の場合は少し面倒です。

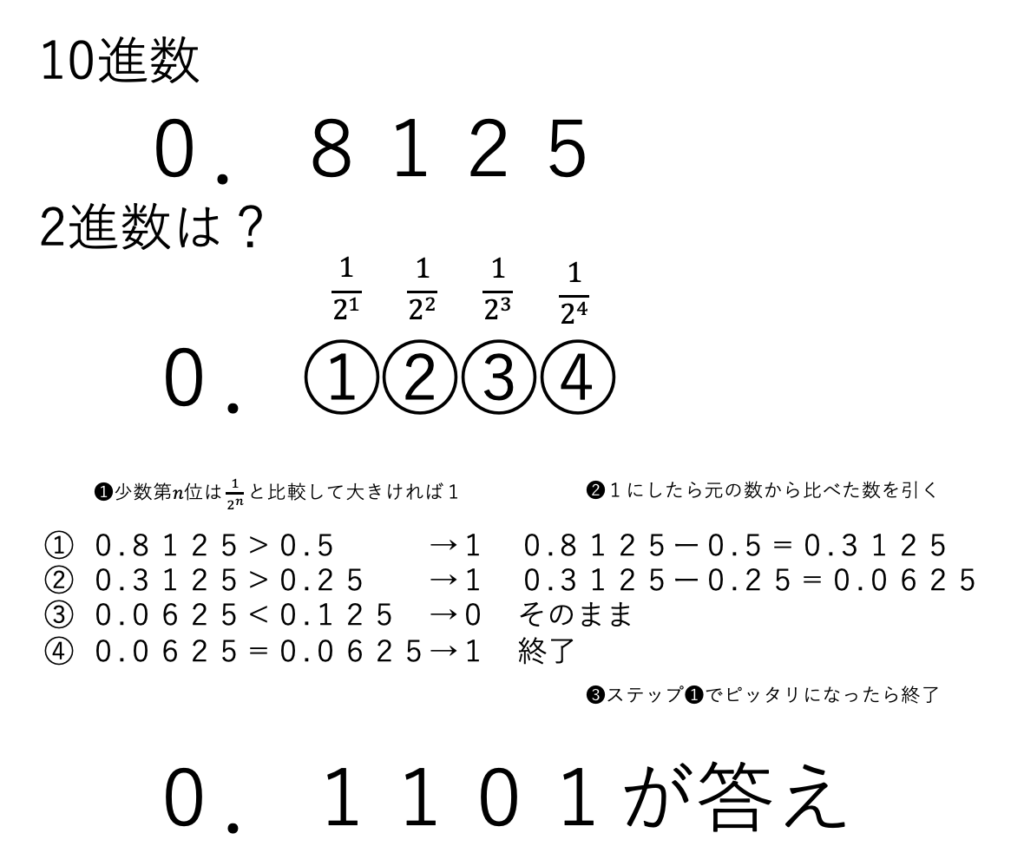
下のイメージを見てください。

10進数の場合、0.1というのは1/10、0.01というのは1/100 = 1/10²でしたね。
2進数の場合は0.1が1/2、0.01が1/4=1/2² になります。

では、0.8125を例に見てみましょう

変換のステップは
❶少数第n位は1/2ⁿと比べて大きければ１（小さければ０）
❷１にした場合は元の数から1/2ⁿを引く
これを繰り返し最後
❸ステップ❶でピッタリになったら終了させます

少し難しいと感じるかもしれませんが、何問か練習すればできるようになると思います！
頑張りましょう。

2進数を10進数にする

10進数に直すときには筆算などは必要ありません。

まず、小学校1年生の時に頭を戻してみてください。
算数の時間に

「７５３は１００が7個と、10を5個と1を3個合わせたものです」

みたいな問題があったと思います。

これは言い換えると753 = 7 × 10² + 5 × 10¹ + 3 × 10⁰ と表すことができます。

2進数でも同じことをやります。

例えば10110を10進数に直してみましょう

10110₍₂₎ = 1 × 2⁴ + 0 × 2³ + 1 × 2² + 1 × 2¹ + 0 × 2⁰

= 1×16 + 0×8 + 1×4 + 1×2 + 0×1

= 16 + 0 + 4 + 2 + 0

= 22

どうでしょう？
10進数と同じ考え方で導けたのではないでしょうか？

少数部分についても同じです。
先ほども述べたように2進数の場合は0.1が1/2、0.01が1/4=1/2² になります。

例えば、0.1101の場合は

0.1101 = 1/2¹ × 1 + 1/2² × 1 + 1/2³ × 0 + 1/2⁴ × 1

= 0.5×1 + 0.25×1 + 0.125×0 + 0.0625

=0.8125

2進数の計算は情報では必須なのでしっかり覚えましょう！

（数学でもどうせ出てくるので覚えちゃえば一石二鳥です）

ではまた！