コンピュータは0と1しか扱うことができないことから2進数で計算を行います。
2進数のことがまだよくわかっていない人は、まずこちらの記事を読んでください。
ここでは、2進数同士の計算を紹介していきます。
共通テストでここまで単純な計算問題はあまり出ないと思いますが、定期テストでは必出といっても過言ではないと思うので、しっかり勉強しておきましょう。
数学でもどうせ使う知識なので今覚えておくと一石二鳥です。
2進数の加算(足し算)
基本的には10進数の時とやり方は同じです。
注目するポイントとしては「繰り上がり」です。
筆算で足し算をするとき、10進数の時は5+6=11のように各位の足し算結果が10を超えたら繰り上げていました。
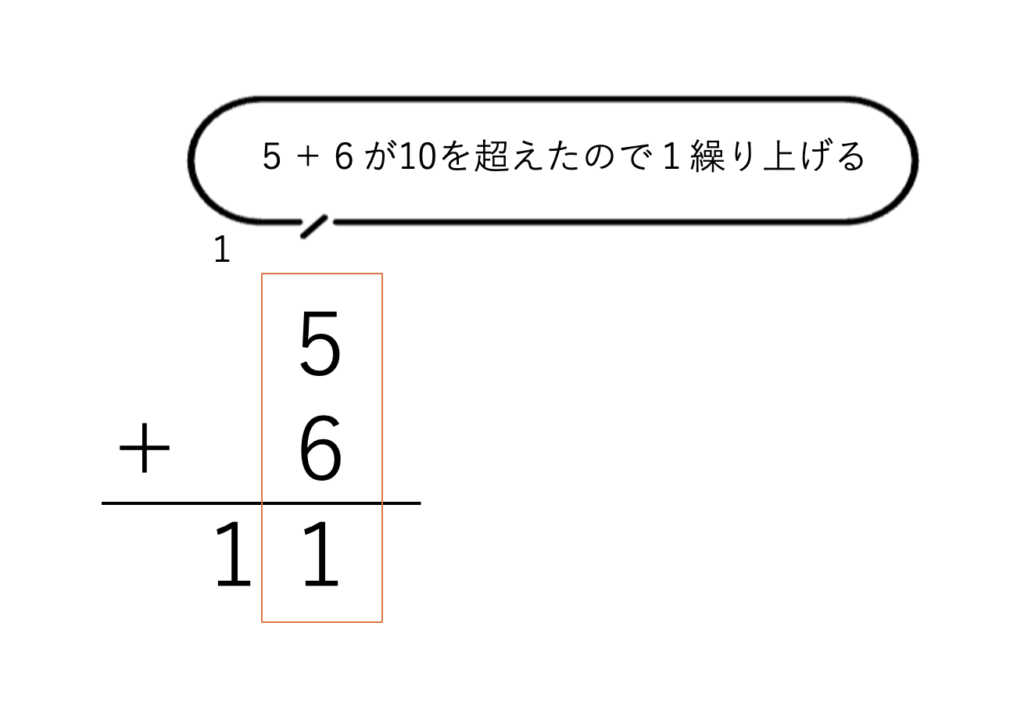
2進数ではその基準が2になります。
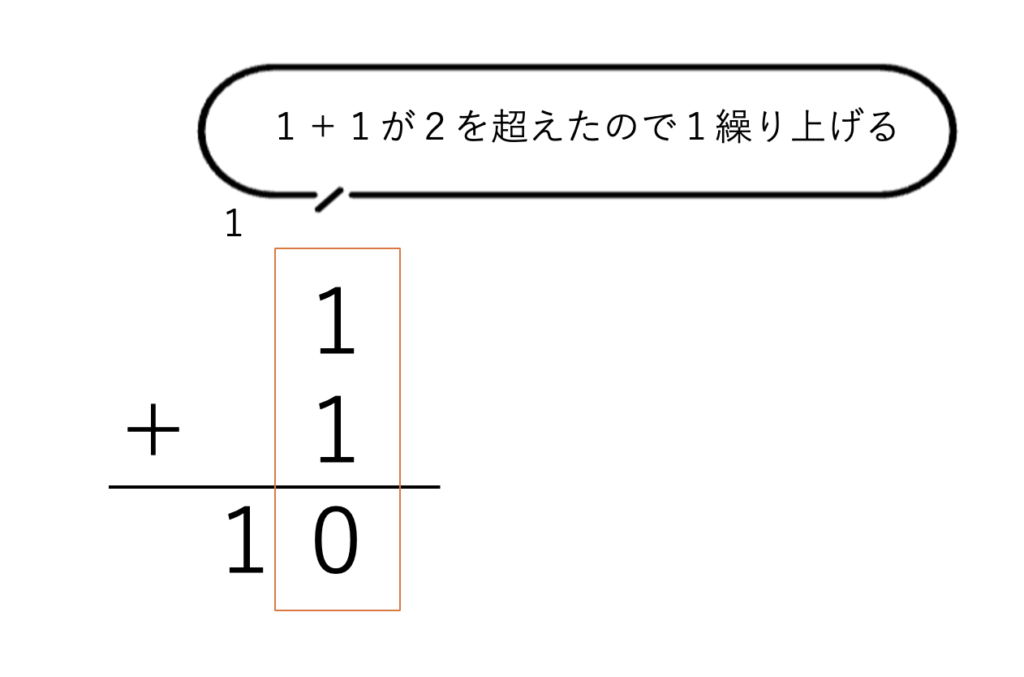
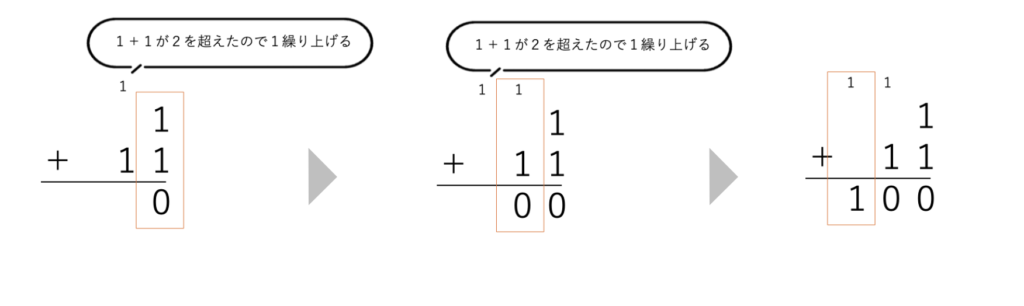
2桁以上になってもやることは変わりません。
繰り上がった1と元々ある数を足すことを繰り返していきます。
2進数の減算(引き算)
引き算も基本的なやり方は10進数の時と変わりません。
注意するのは繰り下がりだけです。
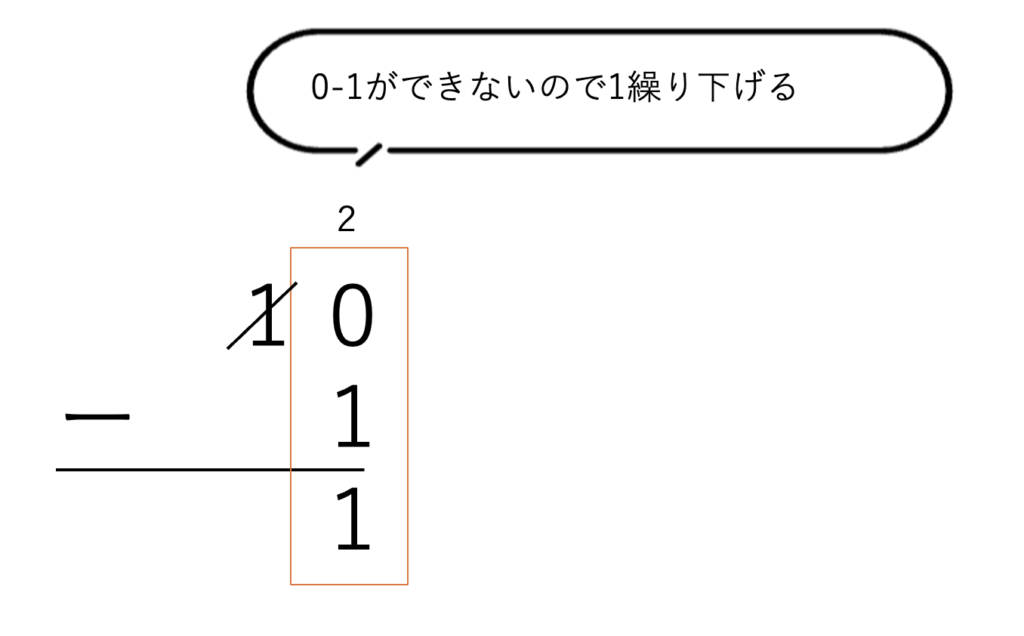
10−1を見てみましょう。
0−1はできないので上の桁から2を借りてきます。
(10進数の時は10借りてきましたよね?)
すると1桁目は2−1=1、2桁目は貸してしまったのでなくなり0−0=0となります。
負の数の表現(補数の考え方)
次は負の数を表現する方法を考えましょう。
負の数を表したい時、コンピュータでは補数というものを使います。
補数とは「ある自然数に対して足すと1桁増える最も小さな数」のことです。
10進数で考えると6の補数は4、99の補数は1になります。
2進数の補数の考え方は2パターンあります。
理解しやすいのはパターン1、使いやすいのはパターン2だと思います。
4ビットの2進数である0101(2)の補数
を求めなさい
パターン1 一つ桁が多い10000から0101を引く
一番シンプルな考え方ですね。
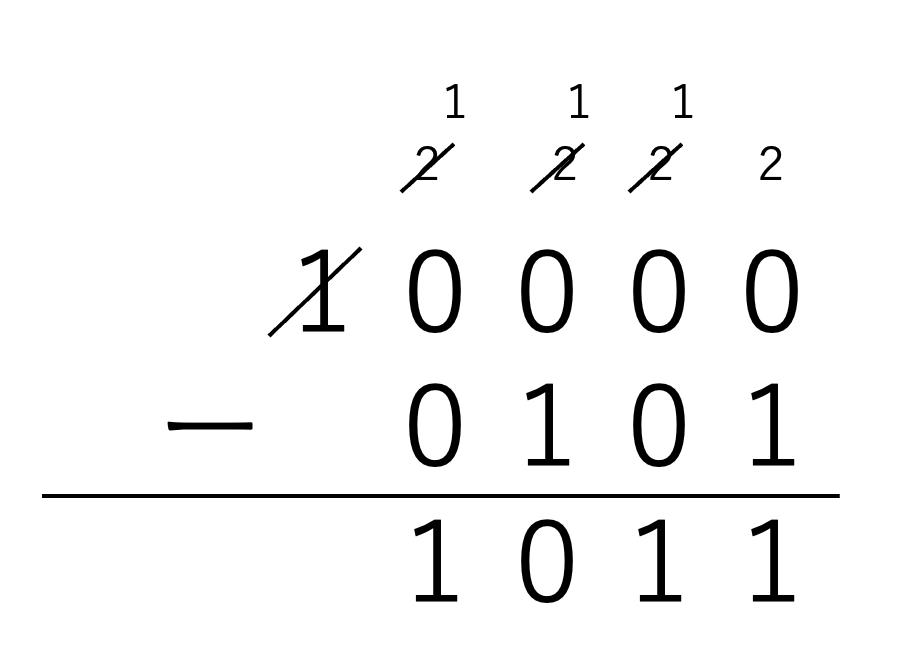
10000ー0101=1011
これは言い換えると
0101+1011=10000となり、足すと一桁増えるので0101の補数は1011となります。
注意点としては、今問題で4ビットの2進数と言われているので0101は先頭の数字が0ですが、3桁ではなく4桁になります。
パターン2 ひっくり返して1を足す
テストで補数を聞かれたらこっちを使ってください。
ステップ1 各位の0と1を反転させる
0101→1010
ステップ2 1を足す
1010+0001=1011
完成!
めっちゃ簡単ですね!
パターン1を使ってもパターン2を使ってもどちらでも解くことができます。
意味はパターン1で理解し、テストではパターン2を使うことがいいと思います。
補数を使った減算(引き算)
さて、最後に補数を使った引き算について説明します。
補数はマイナスを表すということは、元々引き算だったものを補数との足し算として考えることができます。
0111 – 0100 = ?
ステップ1 0100の補数を考える
ここは各位の0と1を交換して1を足しましょう
0100→(ひっくり返す)1011→(1足す)1100
補数が1100であることがわかりました!
ステップ2 0111+1100をする
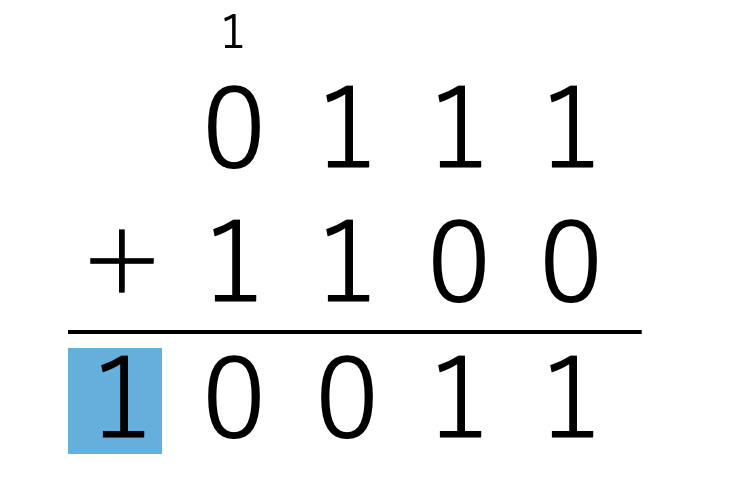
注意点は桁あがりした青枠の1は無視することです。
すると答えが0011であることが分かります。
まとめ
いかがだったでしょうか?
2進数の計算と言われると身構えてしまいますが、やっていることは10進数の算数とさほど変わりません。
繰り上がりや繰り下がりのところだけ注意して練習しましょう!


